LUMIÈRE - Polarisation

LUMIÈRE - Polarisation

Les phénomènes lumineux peuvent, selon la théorie électromagnétique (cf. LUMIÈRE - Optique), être considérés comme liés à la propagation simultanée d’un champ électrique つ et d’un champ magnétique H, constamment perpendiculaires entre eux ainsi qu’à la direction de propagation (fig. 1), et dont les valeurs sont des fonctions sinusoïdales du temps t . On raisonnera ici sur le seul champ électrique, auquel sont dus notamment les effets perçus par l’œil, et qu’on identifie au vecteur lumineux de la théorie de Fresnel.

Le caractère transversal de ce champ électrique est mis en évidence par la possibilité d’extinction complète du vecteur lumineux dans certaines expériences, décrites ci-après, qui montrent que les vibrations n’ont pas de composante parallèle à la direction de propagation. Alors que, pour la lumière dite naturelle, toutes les orientations normales à la vitesse paraissent équivalentes, on peut produire des lumières, dites polarisées rectilignement, pour lesquelles le vecteur représentatif reste parallèle à une direction fixe. Il se peut aussi que son extrémité décrive une ellipse (réduite à l’un de ses axes dans le cas précédent) et, en particulier, un cercle.

Ces lumières elliptiques peuvent résulter de la composition de deux vibrations rectangulaires, réalisées dans des conditions convenables; mais jamais ces vibrations ne peuvent se neutraliser complètement par interférence, alors que cela est possible pour deux faisceaux superposés, vibrant rectilignement suivant la même direction, pourvu, bien entendu, que soient satisfaites les exigences de cohérence de phase ^{[cf. INTERFÉRENCES LUMINEUSES]}.

Certains dispositifs d’étude, d’examen ou d’utilisation des lumières polarisées répondent de façon plus ou moins marquée aux variations de longueur d’onde ; d’autres, sur lesquels on insistera, sont utilisables en lumière complexe, blanche en particulier.

1. Lumières polarisées rectilignement. Loi de Malus

Soit un faisceau de rayons parallèles schématisé par le rayon SI (fig. 2 a) provenant du Soleil ou d’une source artificielle d’émission dite spontanée. Recevons-le sur une surface vitreuse plane M portée par un cylindre circulaire C pouvant tourner dans un second cylindre K d’axe SI. L’intensité du faisceau réfléchi IR ne dépend pas de l’orientation du plan d’incidence SIN: la lumière du faisceau SI est dite naturelle.

Mais la lumière du faisceau réfléchi ne possède pas la même symétrie; car, si on la reçoit en I (fig. 2 b) sur une deuxième surface vitreuse M et si l’on fait tourner celle-ci autour de II , le rayon deux fois réfléchi I R a une intensité périodiquement variable: maximale (deux fois par tour) quand les deux plans d’incidence SIN et II N coïncident, minimale quand ils sont perpendiculaires. Les minimums sont nuls quand les angles d’incidence i et i ont une valeur particulière i ^B (incidence de Brewster) telle que tg i ^B = n (indice du milieu réfléchissant); i ^B est de l’ordre de 55⁰ pour le verre et atteint 74⁰ pour l’oxyde de titane, d’indice voisin de 2,5. Dans le cas de l’incidence brewstérienne, le rayon II est dit polarisé rectilignement , d’une façon complète. M , qui permet de s’en rendre compte, est appelé analyseur , M étant un polariseur . Sous une incidence i différente, II est un mélange de lumière rectiligne et de lumière naturelle.

Si, dans le cas de la polarisation complète, on fait tourner l’analyseur M autour de la direction d’incidence II d’un angle 見 à partir de la position d’extinction (polariseur et analyseur «croisés»), on constate que l’intensité réfléchie I varie suivant la loi:

qui a été établie par E. L. Malus, et qui est valable quels que soient le polariseur et l’analyseur utilisés.

Cette loi s’interprète ainsi: la vibration rectiligne, d’amplitude A, tombant sur l’analyseur, se comporte comme la résultante de deux vibrations rectangulaires de même période, d’amplitudes respectives A sin 見 et A cos 見, dont la seconde est arrêtée par l’analyseur. Ce dernier ne transmet qu’une fraction déterminée de la première correspondant à une intensité 福A² sin² 見 (les intensités étant proportionnelles aux carrés des amplitudes); 福 est un facteur de réflexion, indépendant de 見, qu’il convient, dans d’autres types d’analyseur, de remplacer par un facteur de transmission.

On peut représenter la lumière naturelle comme formée de vibrations rectilignes, émises par les atomes ou les molécules lorsque leur état d’excitation varie (cf. LUMIÈRE - Optique). Ces variations interviennent à des intervalles de temps irréguliers, très grands par rapport aux périodes de vibration T (qui sont de l’ordre de 10^-15 s, alors que la «durée de vie» d’un atome excité est de l’ordre de 10^-9 s), mais très petits par rapport aux temps de réponse des récepteurs de lumière (10^-3 s, parfois beaucoup plus).

Le vecteur de Fresnel:

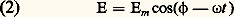(pour lequel 諸 = 2 神/T) varie donc très souvent en direction, en amplitude E^m et en phase 﨏 (celle-ci étant déterminée par la distance du point d’observation O à la source et par l’instant d’émission), sans que ces variations soient perceptibles par les récepteurs. En particulier, sa projection sur un axe quelconque Oxpassant par O est perçue comme ayant une intensité constante, égale à sa valeur moyenne, soit E^2m/2, et indépendante de l’orientation de Ox 轢.

C’est une telle composante, orientée suivant Ox 轢, par exemple, qu’isole un polariseur rectiligne.

Contrairement à ce qui se produit pour l’émission «spontanée» des sources thermiques usuelles, l’émission «induite» ^{[cf. LASERS]} est formée de vibrations rectilignes ayant toutes même direction (et d’ailleurs aussi même phase, pendant un temps relativement long), sans qu’il y ait à interposer un polariseur. Aussi oriente-t-on certains miroirs «de sortie» des cavités lasers en utilisant l’incidence brewstérienne pour que le faisceau soit réfléchi au mieux.

La diffusion par des molécules gazeuses (cf. DIFFUSION DE LA LUMIÈRE - Météorologie) favorise la vibration normale au plan contenant le rayon incident et le rayon diffusé; la polarisation est complète si ces rayons sont perpendiculaires l’un à l’autre. Ainsi, la lumière bleue diffusée par l’atmosphère terrestre se trouve plus ou moins polarisée; elle l’est complètement dans une direction normale à celle du Soleil.

2. Polariseurs et analyseurs

Tout polariseur rectiligne peut servir d’analyseur, et inversement; il n’y a donc pas à étudier deux types d’instruments différents. La réflexion (sous l’incidence brewstérienne) n’est employée qu’exceptionnellement, parce que la fraction réfléchie de lumière naturelle incidente est toujours faible (moins de 10 p. 100 sur du verre) et que la déviation du faisceau est souvent incommode. Le reste du flux, qui est réfracté (aux pertes par absorption près), est constitué d’une fraction de lumière rectiligne vibrant parallèlement au plan d’incidence (alors que la vibration réfléchie lui est normale) et surtout de lumière restée «naturelle».

Le phénomène de double réfraction, qui s’observe dans les cas de la plupart des cristaux transparents (cf. OPTIQUE CRISTALLINE; LUMIÈRE - Réflexion et réfraction), s’accompagne d’une polarisation. Il est particulièrement marqué quand on utilise du spath d’Islande (carbonate de calcium CaCO³). Un rayon de lumière qui traverse un rhomboèdre de spath (fig. 3) donne naissance à un rayon ordinaire (O), qui suit les lois habituelles de la réfraction, et à un rayon dit extraordinaire (E) différemment dévié. Ce dernier vibre dans le «plan de section principale» du cristal (déterminé par son axe optique et par la normale IN à la face d’entrée), tandis que le rayon ordinaire vibre normalement à ce plan. À l’émergence, les deux rayons redeviennent parallèles, en conservant leur état de polarisation.

L’emploi d’un prisme, au lieu d’une lame à faces parallèles, permet de donner aux deux faisceaux émergents des directions différentes, donc de mieux les séparer (à une distance suffisante). À un tel prisme on en associe souvent un autre, de même angle, orienté en sens inverse et non biréfringent (tout au moins dans les conditions où il est taillé et utilisé); c’est le cas, par exemple, des prismes de Rochon (fig. 4).

Le plus souvent, on souhaite n’utiliser qu’un des faisceaux polarisés; on peut éliminer l’autre par réflexion totale sur la face de sortie du prisme, séparé du second par une couche d’air dans le polariseur de Glan et par une couche de baume du Canada dans celui de Nicol (fig. 5), tous deux en spath. Le mot «nicol» est couramment employé pour parler d’un polariseur ou d’un analyseur, quel que soit son type.

Certains cristaux biréfringents, notamment la tourmaline, absorbent l’une des radiations réfractées beaucoup plus fortement que l’autre. En lumière blanche, il peut en résulter des différences de couleur qui font qualifier ces polariseurs de dichroïques .

Des ensembles de très petits critaux dichroïques en suspension dans une matière plastique transparente et tous orientés de la même façon constituent des lames polarisantes dont certaines portent le nom commercial de Polaroïds. Bien qu’elles n’assurent pas une polarisation parfaite et qu’elles soient légèrement colorées, on les emploie de plus en plus, parce qu’on peut les obtenir en assez grandes dimensions, que leur minceur est souvent commode et que leur prix de revient est très inférieur à celui des prismes de spath, minéral qui devient de plus en plus rare.

3. Lumières elliptiques et circulaires

Soit une lame biréfringente mince L, à faces parallèles, d’épaisseur e de l’ordre du centième de millimètre, obtenue, par exemple, en clivant du mica. Si la lumière incidente est naturelle, celle qui émerge l’est aussi. Dans le cas d’une lumière polarisée rectilignement, représentable par un vecteur つ d’amplitude A, la biréfringence sépare des vibrations rectangulaires, représentables par les projections de つ sur deux axes Ox 轢, Oyliés à L, et qui sont appelés ses lignes neutres (cf. OPTIQUE - Optique cristalline, chap. 2). Les amplitudes de ces projections sont respectivement X = A cos 見 et Y = A sin 見, 見 étant l’angle de つ avec Ox(fig. 6). Ces vibrations ont des vitesses différentes correspondant à des indices n ^x et n ^y . Si n ^x 礪 n ^y , le chemin optique de la vibration suivant Oxest plus grand que celui de la vibration Oy 轢. Oxest retardée et l’on appelle Oyl’axe rapide .

À la sortie de la lame, ces vibrations ont pris des retards de phase, 﨏^x et 﨏^y, proportionnels à e . Provenant d’une même source ponctuelle, celles qui sont superposées se composent et l’extrémité du vecteur résultant décrit une ellipse inscrite dans un rectangle de côtés 2 X et 2 Y (fig. 6). On obtient ainsi, en général, une vibration elliptique qui est dite droite ou gauche selon que, pour un observateur recevant la lumière, elle tourne dans le sens des aiguilles d’une montre ou en sens inverse.

Dans le cas particulier où 﨏 = 﨏^y 漣 﨏^x = k 神, avec k entier positif, la lame L est dite onde si k est pair, et demi-onde si k est impair. L’ellipse se réduit alors à l’une des diagonales du rectangle; la vibration émergente est rectiligne, parallèle à つ dans le premier cas et symétrique de つ par rapport aux axes dans le second.

Lorsque 﨏 = (2 k + 1)( 神/2), avec k entier positif, la lame est dite quart d’onde ; l’ellipse a alors Oxet Oypour grands axes. Si de plus X = Y, c’est-à-dire si 見 = 神/4, elle devient un cercle, et l’ensemble du polariseur rectiligne et de la lame L est un polariseur circulaire.

Il existe d’autres modes d’obtention d’une lumière circulaire. La réflexion totale (vitreuse) s’accompagne d’un changement de phase, qui peut être de 神/4 pour un angle d’incidence convenable. Un dispositif où se produisent successivement de telles réflexions (parallélépipède de Fresnel) peut donc remplacer une lame quart d’onde. Il a l’avantage d’être beaucoup mieux achromatique, c’est-à-dire d’être pratiquement insensible aux variations de longueur d’onde.

Une obtention plus directe de lumières circulaires résulte de ce qu’une vibration rectiligne peut être considérée comme la résultante de deux vibrations circulaires, d’amplitudes égales, tournant en sens inverse (cf. infra ). Les corps doués de pouvoir rotatoire (cf. OPTIQUE CRISTALLINE, chap. 3), tel le quartz dans la direction de son axe optique, peuvent, convenablement taillés, produire ce dédoublement; la séparation angulaire étant très faible, Fresnel a utilisé un ensemble de prismes disposés comme l’indique la figure 7. Si la lumière incidente est naturelle, les deux lumières circulaires émergentes subissent comme elle des variations de phase aléatoires, et sont donc incohérentes, à l’échelle des récepteurs.

L’action d’un analyseur A rectiligne sur un faisceau de lumière s’explique toujours par la transmission d’une composante de cette lumière, comme il a été indiqué à propos de la loi de Malus (cf. chap. 1). Les divers cas qu’il est possible de reconnaître en employant au besoin une lame quart d’onde, en plus de A, sont présentés dans le tableau 1.

4. Matrices de Jones

Le calcul matriciel (cf. algèbre LINÉAIRE ET MULTILINÉAIRE) peut être avantageusement utilisé pour l’étude des phénomènes de polarisation. Deux axes rectangulaires Ox 轢, Oyétant choisis, on peut associer à une vibration lumineuse rectiligne, d’amplitude A, faisant avec Oxl’angle , une matrice à une colonne:

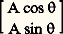avec comme cas particuliers:

Une vibration elliptique, inscrite dans un rectangle de côtés 2 X et 2 Y parallèles aux axes, et dont les composantes ont des phases 﨏^x et 﨏^y , est associée à une matrice: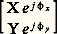

e étant la base des logarithmes népériens et j le symbole complexe 漣 1. Dans le cas particulier des vibrations circulaires, en posant 﨏^x 漣 﨏^y = 神/4 et X = Y = 1, le sens de rotation peut être gauche ou droite, et les matrices correspondantes s’écrivent:

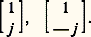La composition de deux lumières de polarisation donnée s’étudie par addition de leurs matrices. Par exemple, pour des vibrations circulaires de sens inverses:

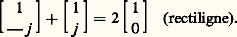Un système optique linéaire peut être caractérisé par une matrice carrée, dite de Jones, comme l’indique le tableau 2.

Après traversée d’une succession de systèmes dont les matrices caractéristiques de Jones sont :

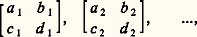une vibration incidente:

devient: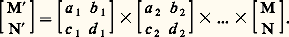

Par exemple, lorsqu’une vibration rectiligne à 45⁰ des axes, soit:

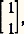traverse une lame quart d’onde dont l’axe rapide est parallèle à Ox 轢, soit:

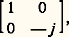le vecteur transmis est:

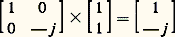(vibration circulaire droite).

5. Applications

Les études sur la polarisation de la lumière ont apporté une contribution essentielle à nos connaissances sur les vibrations lumineuses. Elles trouvent de nombreuses applications comme:

– La détermination de la polarisation des sources optiques. Les lasers ont une polarisation rectiligne permanente alors que les sources thermiques émettent des vibrations rectilignes incohérentes: les directions, les amplitudes, les phases, sont aléatoires en fonction du temps (cf. LUMIÈRE - Optique).

– La détermination des caractéristiques optiques de la matière où l’indice peut être réel ou complexe, avoir une forme scalaire ou tensorielle. En effet, le vecteur polarisation d’une onde se modifie par réflexion, réfraction (isotrope ou anisotrope), absorption, diffusion... (cf. LUMIÈRE - Réflexion et réfraction). Des changements de l’état de polarisation peuvent apparaître brutalement par induction. Ces propriétés sont utilisées pour fabriquer des interrupteurs, des déflecteurs, des modulateurs (de phase et d’amplitude) ultrarapides employés en «optique guidée» et «optique intégrée» (cf. TÉLÉCOMMUNICATIONS OPTIQUES - Télécommunications optiques).

L’analyse des vibrations se fait par ellipsométrie; un ellipsomètre comprend essentiellement un banc d’optique sur lequel sont disposés un polariseur rectiligne, le corps à étudier et un analyseur permettant de déterminer les caractéristiques des vibrations elliptiques (orientation, ellipticité, sens de parcours).

Les interférences en lumière polarisée servent à déterminer des biréfringences naturelles et artificielles, à étudier certains matériaux, certains tissus, etc., dont l’examen entre polariseur et analyseur croisés (ou encore parallèles) fait apparaître, en lumière parallèle ou convergente, des aspects colorés dus aux variations d’épaisseurs, au phénomène de double réfraction ou aux inégales transmissions des diverses longueurs d’onde (cf. OPTIQUE CRISTALLINE et MICROSCOPES).

Enfin, le phénomène de polarisation rotatoire permet les dosages polarimétriques de substances optiquement actives telles que les solutions de sucre.

Encyclopédie Universelle. 2012.